2 剛床仮定での建物の変形と偏心率
剛床仮定が成り立つ場合、水平構面自身の変形の影響は考えなくてよいので、水平構面の移動は耐力壁の剛性と配置のみで決まります。このときの建物のねじれ剛性に対する耐力壁の抵抗力の合力と建物の重心のずれ(ねじり力の強さ)の度合いを偏心率といいます。弾性変形の範囲では、偏心によって耐力壁に生じる力は外力に比例するので、偏心率を使えば偏心によるねじれ力を簡単に表現できます。
下図(Fig.2-3)は水平力を受ける建物をモデル化したものです。今Y軸(紙面上下)方向に力がかかっています。
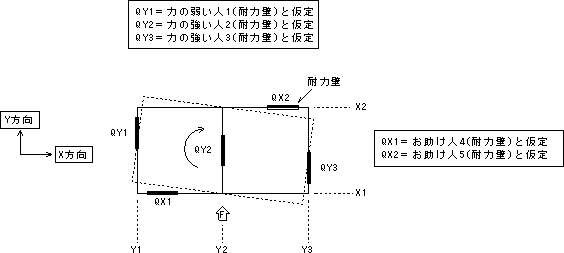 |
| Fig.2-3 水平力構面のモデル |
最初の段階では建物全体が弾性状態です。水平力に対してはY方向の耐力壁が、ねじり力に対してはXY両方の壁が抵抗しています。
次に建物の変形が大きくなって耐力壁が塑性状態に入った場合の偏心による影響について考えます。耐力壁の荷重−変形関係は完全弾塑性だとします。
水平力が増大してY通りの耐力壁がすべて降伏した(受けている力は一定なままで変形が増大していく)とします。そうなると偏心によるねじれ力に対してはX通りの耐力壁だけしか抵抗できません。
従って、塑性状態にはいってからは、建物のねじれ角はX通りの耐力壁の回転剛性によって決定されます。
もっとわかりやすい図(Fig.2-4)で説明すると
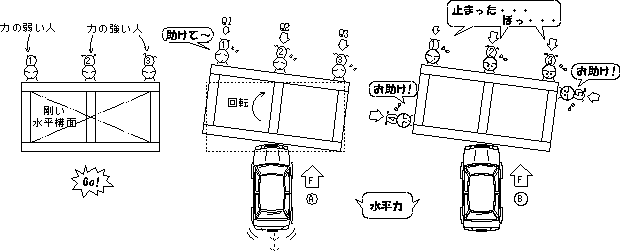 |
| Fig.2-4 水平力構面のモデル2 |
A図で車の押す力Fによって移動しようとする箱を1〜3の三人が支えているとします。1の人が弱く少しの力しか支えられないと、Aのように他の二人が強くても支える力が違うので箱はバランスを崩して回転しようとします。押す力が小さいうちは2が回転を止めようとしますが、力が大きくなると他の二人の靴も滑り出し、ある一定以上の力は支えられなくなり、回転も止まらなくなります。
そこで、Bのように直交から4と5のように支えてやれば(直交壁が有効な耐力壁であれば)回転しようとする力を止めることができます。
これと同じことが鉛直構面と建物質量に生じる地震力の間でもいえます。
※本当は動いているときと止まっているときでは摩擦力が違うので弾塑性モデルにならないが、ねじれの説明としてはわかりやすいので、あえてこのように説明しています。
このようにして建物が変形する場合、その中のいずれかの耐力壁の変位が、限界(終局状態もしくは限界変形角)に達したときが、建物全体の終局状態になります。
剛床(変形しない)だと、耐力壁の変位分布は直線状になり、各鉛直構面ごとの変位は求めやすくなります。これと各鉛直構面の荷重−変位性能(Fig.2-5)から最も最初に限界に達する耐力壁線を求めれば、そのときの耐力壁の耐力の和が建物全体の耐力となります。
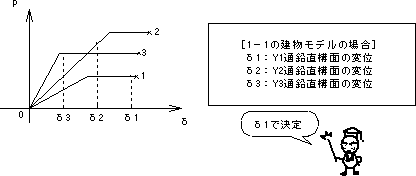 |
| Fig.2-5 各鉛直構面の荷重−変形関係とある時点での変位 |